Két Vektor Skaláris Szorzata - Koordinátáival Adott Vektorok Skaláris Szorzatának Kiszámítása | Matekarcok
FELADAT Állítsd be úgy a B és C pontokat, hogy a BOC 90 o legyen! Keresd meg az A pont olyan helyzeteit, amikor A' és A nem esik egybe! Hány különböző pont tesz eleget ennek a feltételnek? Miért? Definíció szerint: =λ +μ, ahol λ= * és μ= *. Pl. : -ral skalárisan szorozva: * =λ * +μ *. Ha * =0, vagyis merőlegesek, megkapjuk a λ együtthatót. A' definíciója szerint viszont λ= *, de ekkor, rendezve:( -)* =0 Mivel nem nulla, és irányát megválaszthattuk, tehát nem tehető fel, hogy merőlegesek, ezért - =0, vagyis A és A' ilyenkor mindig egybeesik. KAPCSOLÓDÓ ÉRDEKESSÉGEK Legyen β = 60 o és γ = 120 o. Ekkor az első koordináta a felére csökken, a második a másfélszeresére nő. Ha ügyes vagy, jól megy a vektorfelbontás, és alkalmazod a skaláris szorzás azonosságait, ezt az összefüggést rövid számolással ellenőrizheted. Tipp: Az =( *)* +( *)* összefüggésben az és vektorokat írjuk fel a szokásos bázisban, valamint vegyük észre, hogy nevezetes szögekkel dolgozunk. Legyen a BOC 90 o -tól különböző! Mozgassuk egy egyenes mentén – a könnyű beállítás miatt például szomszédos rácspontokon – A-t. Hogyan mozog ekkor A'?
- Fejezze ki két vektor skaláris szorzatát a vektorok koordinátáinak segítségével! - Matematika kidolgozott érettségi tétel - Érettségi.com
- Skaláris szorzás definíciója | Matekarcok
Fejezze ki két vektor skaláris szorzatát a vektorok koordinátáinak segítségével! - Matematika kidolgozott érettségi tétel - Érettségi.com
(belső szorzatot). Általános értelemben egy adott vektortér felett bármely kétváltozós leképezést belső szorzatnak nevezünk, ha a fenti tulajdonságokat teljesíti. Egy vektortér felett akár több különböző belső szorzat is definiálható. Ilyenkor inkább szokásos a jelölés. Példák [ szerkesztés] Az intervallumon folytonos, -be képező függvények terén értelmezett belső szorzat: Komplex értékű függvények esetén az integrandus -ra módosul. Bármely lineáris térben értelmezhető egy adott bázishoz tartozó skalárszorzat a következőképp. Ha és vektor az bázisban felírható: akkor az ezen bázis által meghatározott skalárszorzat: Geometriai vonatkozások [ szerkesztés] Az euklideszi geometriában szoros összefüggés áll fenn a skalárszorzat és a hosszak, valamint a szögek között. Egy vektorra a hosszának (abszolút értékének) négyzete, és ha egy másik vektor, akkor ahol és jelöli az és vektor hosszát, pedig az általuk bezárt szög. Mivel az vektornak -re való vetülete, a skalárszorzatot geometriailag úgy lehet értelmezni, mint -nak irányába eső komponensének és -nek a szorzatát.
Ha két vektor merőleges egymásra, akkor hajlásszögük koszinusza 0, így skaláris szorzatuk is nulla. Megfordítva, ha két, egymással szöget bezáró (nem nulla hosszúságú) vektor skaláris szorzata nulla, akkor és így. Követve azt a konvenciót, hogy a nullvektor minden vektorra merőleges, a fentieket úgy foglalhatjuk össze, hogy két vektor akkor és csak akkor merőleges, ha a szorzatuk nulla. A skaláris szorzat szimmetrikus (a műveleteknél megszokott szóhasználattal: kommutatív), mivel Egy vektor önmagával vett skaláris szorzata a vektor hosszúságának a négyzete: Ebből következően, és akkor és csak akkor, ha Az ilyen leképezéseket pozitív definit nek nevezzük. Bilinearitás [ szerkesztés] A skalárszorzat bilineáris, azaz mindkét változójában lineáris. Ez azt jelenti, hogy tetszőleges skalárra és vektorokra (B1) és (B2). A szimmetriatulajdoság miatt ezekből már következik, hogy (B3) és (B4). (B1) közvetlenül következik a definícióból, hiszen) Általánosítás [ szerkesztés] Általában bármely vektortér felett értelmezhetünk skalárszorzatot [ forrás? ]
Azaz �s helyvektorok eset�n: 1. 3. K�t vektor k�l�nbs�ge ( Subtraction) Az k�l�nbs�gvektor�n az �sszegvektort �rtj�k, azaz azt a vektort, amelyet �gy kapunk, hogy a -hoz hozz�adjuk b ellentettj�t. Ha az a �s b vektorokat egy pontb�l ind�tjuk ki, akkor a b v�gpontj�b�l az a v�gpontj�ba mutat� vektor az. 1. 4. Vektorok k�l�nbs�ge Tulajdons�gai: A kivon�s nem kommutat�v, �s nem asszociat�v művelet. Ha nullvektort vonunk ki egy a vektorb�l, visszakapjuk az a vektort: Ha a nullvektorb�l vonjuk ki az a vektort, akkor az a vektor ellentettj�hez jutunk: Ha egy vektorb�l �nmag�t vonjuk ki a művelet 0 vektort eredm�nyez: Helyvektorok k�l�nbs�g�nek koordin�t�it az egyes vektorok megfelelő koordin�t�inak k�l�nbs�ge adja. 4. Vektor szorz�sa sz�mmal (skal�rral) ( Scalar multiplication) Adott egy a vektor �s egy sz�m. Az a vektor sz�mszoros�n a k�vetkező vektort �rtj�k: Ha vagy, akkor Ha �s, akkor hossz�s�g� vektort kapunk, melynek ir�nya: eset�n a -val megegyező, eset�n a -val ellent�tes. Teh�t egy vektornak egy sz�mmal val� szorzata a vektor hossz�nak n�veked�s�t vagy cs�kken�s�t vonja maga ut�n.
K�t vektor skal�ris szorzata akkor �s csak akkor 0, ha a k�t vektor merőleges egym�sra. Teh�t ha merőlegesek, akkor skal�ris szorzatuk nulla, ha pedig a skal�ris szorzatuk nulla, akkor merőlegesek. A der�ksz�gű Descartes-f�le koordin�ta rendszerben a p�rhuzamos egys�gvektorok skal�ris szorzatainak �rt�ke egys�g, m�g az egym�sra merőleges egys�gvektorok skal�ris szorzatai nulla �rt�ket ad: A vektorok skal�ris szorzat�nak eredm�nye a koordin�ta komponensekkel is megadhat�, ha figyelembe vessz�k az egys�gvektorok skal�ris szorzataira vonatkoz� �sszef�gg�seket. �gy az �s helyvektorok skal�ris szorzata a k�vetkező alakban �rhat�: Az irodalomban a skal�ris szorzatra a z�r�jeles ill. az als�pont jel�l�st is szok�s haszn�lni: 1. 6. P�ld�k skal�ris szorz�s haszn�lat�ra [ 105] K�t vektor hajl�ssz�g�nek kisz�m�t�sa: A skal�ris szorz�s leg�ltal�nosabb haszn�lata k�t vektor hajl�ssz�g�nek a meghat�roz�sa. Hajl�ssz�get sz�molunk p�ld�ul �rny�kol�sn�l, vagy l�that�s�gi tesztel�sn�l. �rny�kol�sn�l a f�ny ir�nyvektora �s a fel�leti norm�lis sz�g�t sz�m�tjuk ki, m�g l�that�s�gi vizsg�latn�l a n�zeti ir�ny, illetve a fel�leti norm�lis �ltal bez�rt sz�g sz�ks�ges.
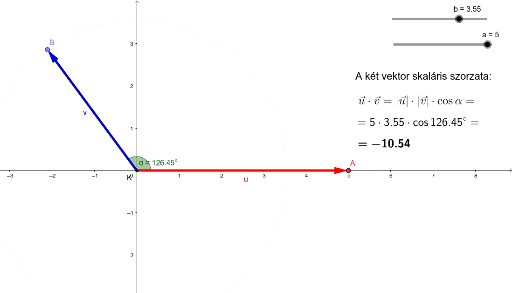
11. évfolyam Skaláris szorzattal vektorfelbontási tétel merőlegesség KERESÉS Információ ehhez a munkalaphoz Szükséges előismeret Vektorok lineáris kombinációja, vektorfelbontási tétel, skaláris szorzás Módszertani célkitűzés A cél bemutatni, hogy skaláris szorzattal kifejthetünk vektorokat tetszőleges ortonormált bázisban. Az alkalmazás nehézségi szintje, tanárként Könnyű, nem igényel külön készülést. Felhasználói leírás Kísérletezz! Milyen beállítások mellett egyezik meg A és A'? Hogyan kaptuk az A'pontot? Először nézzük a problémát a szokásos koordináta-rendszerben, bázisvektoraink (1, 0) és (0, 1), valamint (a1, a2). Ezt skalárisan szorozva -vel, a szorzat: * =1*a 1 +0*a 2 =a 1. Nyilván a -vel vett szorzást hasonlóan elvégezve az a 2 koordinátát kapjuk. Tehát lineáris kombinációval felírható, hogy =( *) +( *) Az A'-t és lecserélésével kapjuk, =( *)* +( *)* tehát helyett az és helyett az egységvektorokkal az előbbihez hasonló formula szerint. A feladatod megvizsgálni, milyen feltétel szükséges ahhoz, hogy A és A' egybeessen.
Skaláris szorzás definíciója | Matekarcok
Ismert, hogy ha egy test valamilyen erő hatására a kérdéses erő irányába elmozdul, akkor az erő által végzett munka (a test mozgási energiájának növekedése) az erő és az elmozdulás szorzata. Az erő és az elmozdulás azonban egyaránt vektormennyiségek, és előfordulhat, hogy irányuk nem esik egybe. Ilyenkor az erő által végzett munka továbbra is lineáris függvénye mind az erőnek, mind az elmozdulásnak, de a munka tényleges mértékének kiszámításában csak az erőnek az elmozdulás irányába eső komponense játszik szerepet. Ha jelöli az erővektor és az elmozdulásvektor hajlásszögét, akkor ez a komponens épp az erővektor -szorosa, így az erő által végzett munka, és skaláris szorzata. Az analitikus geometriában először Lagrange 1773-as, Solutions analytiques de quelques problèmes sur les pyramides triangulaires [4] című művében bukkan fel a skaláris szorzat. A fogalom modern tárgyalása Gibbs 1901-es (tanítványa, Edwin Bidwell Wilson által lejegyzett) Vector Analysis című művében jelenik meg. [5] Alapvető tulajdonságai [ szerkesztés] A skalárszorzat definíciójából közvetlenül következnek az alábbi tulajdonságok.
- Két vektor skaláris szorzata, emelt szintű matematika tételek - YouTube
- Indavideo romantikus filmek videa
- Demjén barlangfürdő átadás
- Tokaj horgony vendéglő
- Magzatvíz szivárgás betét
- Miss ara esküvőszalon vác v
- Skaláris szorzás vektorkoordinátákkal | zanza.tv
- Autópálya matrica 2019 pdf
- Két vektor skaláris szorzata | zanza.tv
- 1.2. Műveletek vektorokkal
- Strand fesztivál program za

Két koordinátáival adott vektor, a (a1, a2) és b (b1, b2) skaláris szorzata: a*b =a1*b1 +a2*b2. Bizonyítás: a =a1*i +a2*j, b =b1*i +b2*j, a*b =(a1*i +a2*i)*(b1*i +b2*i). A disztributív tulajdonság alapján a szorzás tagonként végezhető: a*b =a1*b1*i^2 +a1*b2*i*j +a2*b1*j*i +a2*b2*j^2, i*j =j*i =0, mivel i és j merőlegesek egymásra. i^2 =|i|*|i|*cos(0) =1. Hasonlóan (j^2) is 1-gyel egyenlő. Így a*b =a1*b1*1 +a2*b2*1, amigől a*b =a1*b1 +a2*b2, ezt akartuk bizonyítani. Tehát két vektor skaláris szorzata megfelelő koordinátái szorzatának összege.